Variational Autoencoders (VAEs): A Complete Tutorial
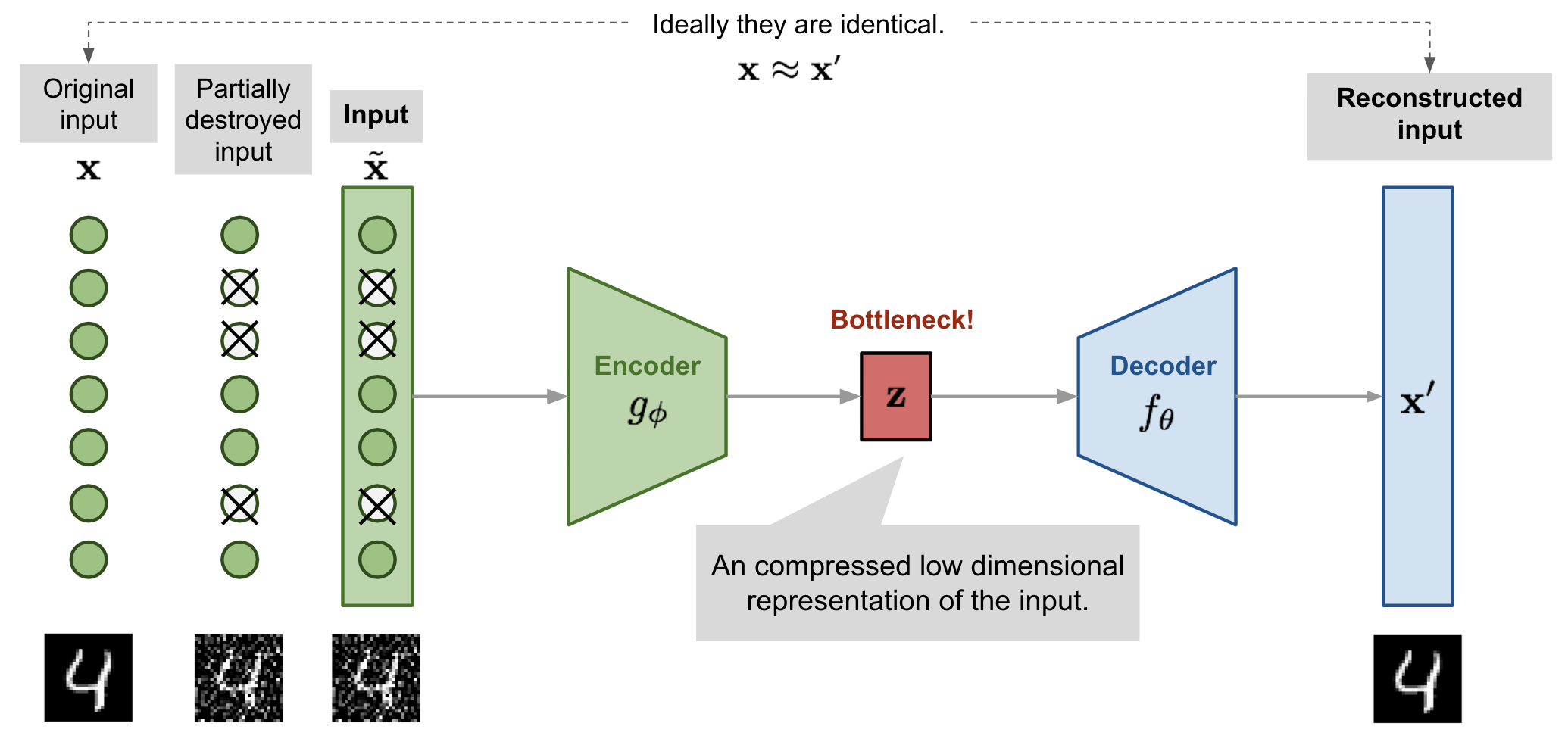
Fig. 1 the structure of variational autoencoder.
🔧 Problem Statement: Why Do We Need VAEs?
We want to learn a generative model that can:
- Sample new data (e.g., images, audio)
- Learn interpretable latent variables
- Model uncertainty in data
We assume the observed data $x$ is generated from a latent variable $z$ using the process:
- Sample $z \sim p(z)$ from a known prior (e.g., $\mathcal{N}(0, I)$)
- Sample $x \sim p_\theta(x \mid z)$
This gives the marginal likelihood:
\[(1) \quad p_\theta(x) = \int p_\theta(x \mid z) \cdot p(z) \, dz\]However, this integral is intractable. To train the model, we need a way to estimate or bound $p_\theta(x)$.
❓ Why Not Just Sample from the Prior and Decode?
We can sample $z \sim p(z)$ and decode to $x \sim p_\theta(x \mid z)$. But to train the decoder, we need to:
- Know what $z$ should produce which $x$
- Learn from real $x$’s, which requires recovering a corresponding $z$
But $z$ is unobserved. We don’t know it. To learn the decoder, we must infer $z$ from $x$. That is, we need the posterior $p_\theta(z \mid x)$, which is intractable because:
\[(2) \quad p_\theta(z \mid x) = \frac{p_\theta(x \mid z) p(z)}{p_\theta(x)}\]And $p_\theta(x)$ involves the same intractable integral from (1).
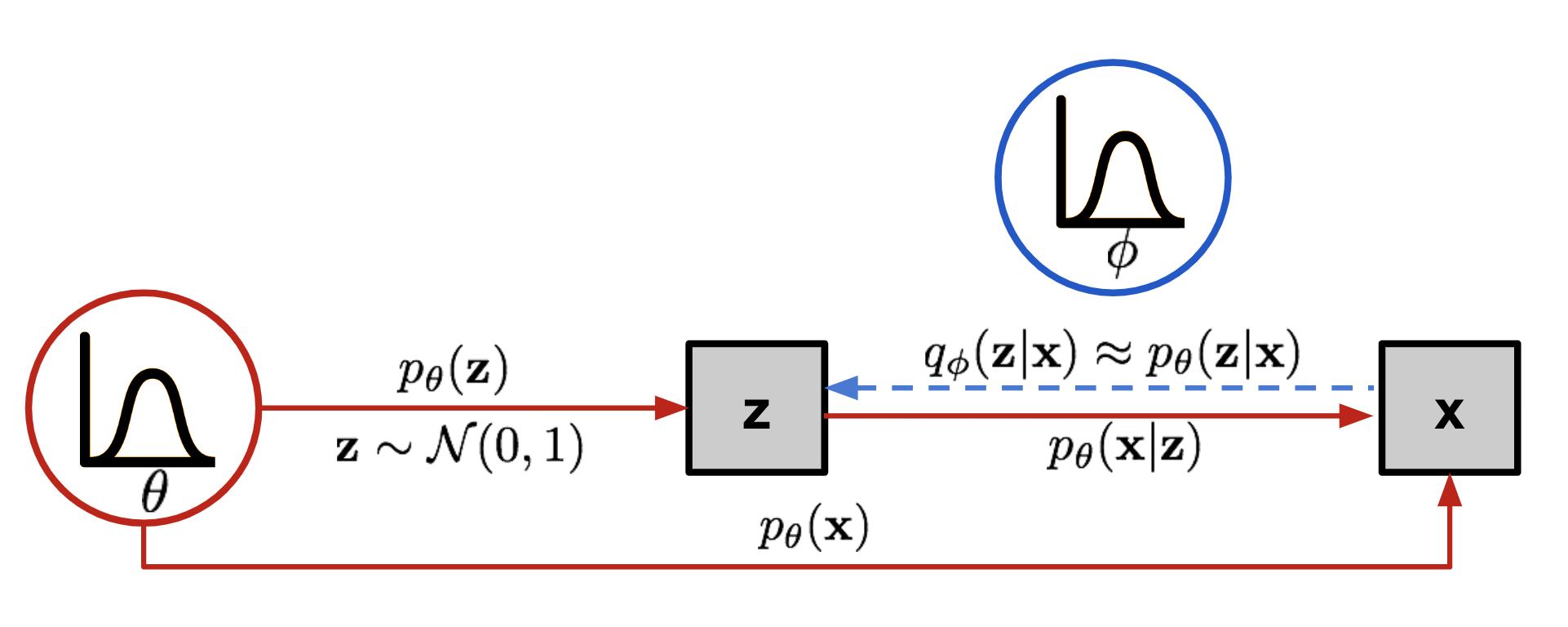
Fig. 2 posterior approximation in vae.
✨ Solution: Approximate the Posterior with an Encoder
We introduce an approximate posterior:
\[(3) \quad q_\phi(z \mid x) \approx p_\theta(z \mid x)\]This encoder network maps $x$ to a distribution over $z$:
\[(4) \quad q_\phi(z \mid x) = \mathcal{N}(z \mid \mu_\phi(x), \sigma^2_\phi(x) I)\]Now we can train both:
- Encoder to approximate the posterior
- Decoder to reconstruct $x$ from $z$
⚡ Derivation of the ELBO
We want to maximize the data likelihood:
\[(5) \quad \log p_\theta(x) = \log \int p_\theta(x \mid z) p(z) dz\]Introduce $q_\phi(z \mid x)$ and rewrite:
\[(6) \quad \log p_\theta(x) = \log \int q_\phi(z \mid x) \cdot \frac{p_\theta(x, z)}{q_\phi(z \mid x)} dz\]Apply Jensen’s inequality:
\[(7) \quad \log p_\theta(x) \geq \mathbb{E}_{q_\phi(z \mid x)} \left[ \log \frac{p_\theta(x, z)}{q_\phi(z \mid x)} \right]\]This is the Evidence Lower Bound (ELBO):
\[(8) \quad \mathcal{L}(\theta, \phi; x) = \mathbb{E}_{q_\phi(z \mid x)}[\log p_\theta(x \mid z)] - D_{\text{KL}}(q_\phi(z \mid x) \| p(z))\]- The first term encourages accurate reconstruction
- The second term regularizes $q_\phi(z \mid x)$ to stay close to the prior $p(z)$
🌈 Reparameterization Trick
We reparameterize $z$ to allow backpropagation:
\[(9) \quad z = \mu_\phi(x) + \sigma_\phi(x) \cdot \epsilon, \quad \epsilon \sim \mathcal{N}(0, I)\]This makes $z$ a differentiable function of $x$ and $\epsilon$.
🧮 KL Divergence Between Two Gaussians
We compute the KL divergence between the approximate posterior $q(z \mid x) = \mathcal{N}(\mu, \sigma^2)$ and the prior $p(z) = \mathcal{N}(0, 1)$ using the closed-form expression:
\[(10) \quad D_{\text{KL}}(q(z \mid x) \| p(z)) = \frac{1}{2} \sum \left( \mu^2 + \sigma^2 - \log \sigma^2 - 1 \right)\]Since we often work with $\log \sigma^2$ (denoted logvar), we rewrite:
This gives the exact PyTorch implementation:
kl = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
logvaris $\log \sigma^2$torch.exp(logvar)gives $\sigma^2$mu.pow(2)gives $\mu^2$
This derivation allows efficient and exact KL computation between two diagonal Gaussians. Let me know if you want me to try inserting this again using a different method.
🔢 Summary
| Concept | Role |
|---|---|
| $p(z)$ | Prior: fixed $\mathcal{N}(0, I)$ |
| $p_\theta(x \mid z)$ | Decoder: likelihood of data given latent |
| $q_\phi(z \mid x)$ | Encoder: approximate posterior |
| ELBO | Training objective maximizing a lower bound on $\log p(x)$ |
By maximizing the ELBO, we can jointly train encoder and decoder networks to form a generative model that both reconstructs input data and regularizes its latent space.
💡 Example: VAE Training Loop for MNIST (With Defined Encoder and Decoder)
import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.utils.data import DataLoader
from torchvision import datasets, transforms
# Define Encoder: x ➝ μ, logσ²
class Encoder(nn.Module):
def __init__(self, latent_dim):
super().__init__()
self.fc1 = nn.Linear(784, 256) # (N, 784) ➝ (N, 256)
self.fc_mu = nn.Linear(256, latent_dim) # (N, 256) ➝ (N, latent_dim)
self.fc_logvar = nn.Linear(256, latent_dim) # (N, 256) ➝ (N, latent_dim)
def forward(self, x):
x = x.view(-1, 784) # reshape input to (N, 784)
h = F.relu(self.fc1(x)) # (N, 784) ➝ (N, 256)
return self.fc_mu(h), self.fc_logvar(h) # both: (N, latent_dim)
# Define Decoder: z ➝ x̂
class Decoder(nn.Module):
def __init__(self, latent_dim):
super().__init__()
self.fc1 = nn.Linear(latent_dim, 256) # (N, latent_dim) ➝ (N, 256)
self.fc2 = nn.Linear(256, 784) # (N, 256) ➝ (N, 784)
def forward(self, z):
h = F.relu(self.fc1(z)) # (N, latent_dim) ➝ (N, 256)
x_hat = torch.sigmoid(self.fc2(h)) # (N, 256) ➝ (N, 784)
return x_hat.view(-1, 1, 28, 28) # reshape to (N, 1, 28, 28)
# Reparameterization trick
def reparameterize(mu, logvar):
std = torch.exp(0.5 * logvar) # (N, latent_dim)
eps = torch.randn_like(std) # (N, latent_dim)
return mu + eps * std # (N, latent_dim)
# VAE class combining encoder and decoder
class VAE(nn.Module):
def __init__(self, latent_dim):
super().__init__()
self.encoder = Encoder(latent_dim)
self.decoder = Decoder(latent_dim)
def forward(self, x):
mu, logvar = self.encoder(x) # ➝ (N, latent_dim) each
z = reparameterize(mu, logvar) # ➝ (N, latent_dim)
x_hat = self.decoder(z) # ➝ (N, 1, 28, 28)
return x_hat, mu, logvar
# Loss function (ELBO)
def loss_fn(x_hat, x, mu, logvar):
recon = F.binary_cross_entropy(x_hat, x, reduction='sum')
kl = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
return recon + kl
# Data pipeline
transform = transforms.ToTensor()
dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
dataloader = DataLoader(dataset, batch_size=128, shuffle=True)
# Training loop
vae = VAE(latent_dim=20)
optimizer = torch.optim.Adam(vae.parameters(), lr=1e-3)
for epoch in range(10):
total_loss = 0
for x, _ in dataloader:
x_hat, mu, logvar = vae(x)
loss = loss_fn(x_hat, x, mu, logvar)
optimizer.zero_grad()
loss.backward()
optimizer.step()
total_loss += loss.item()
print(f"Epoch {epoch+1}, Loss: {total_loss:.2f}")
This full training loop includes an encoder that maps inputs to a distribution over latent variables, a decoder that reconstructs inputs, and a reparameterization trick to enable gradient flow.

