Sample Code for Diffusion Model Training and Inference

In this guide, we’ll provide sample code for training and inference of a diffusion model, specifically focusing on a Denoising Diffusion Probabilistic Model (DDPM). We’ll define the structure for the encoder and decoder using a simplified UNet architecture. Each line of code includes inline comments explaining its purpose, along with the tensor shapes.

Note: This is a simplified example for educational purposes. In practice, diffusion models can be more complex.

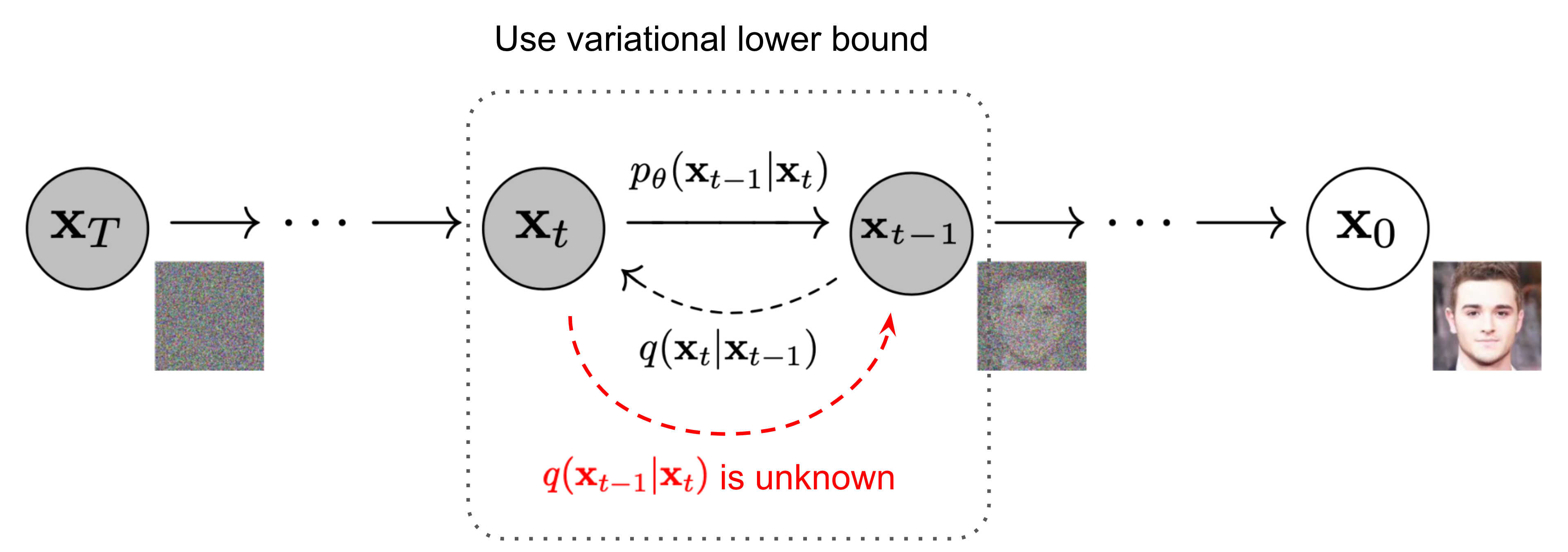
Diffusion

Imports and Setup
Model Architecture (UNet)
Training the Diffusion Model
Inference (Sampling from the Model)
Conclusion
References

Imports and Setup

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import matplotlib.pyplot as plt

Purpose: Import necessary libraries.
- torch, torch.nn, etc.: For building and training the neural network.
- torchvision: For datasets and transformations.
- matplotlib: For visualizing results.

# Device configuration
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")

Purpose: Set the device to GPU if available, else CPU.

Model Architecture (UNet)

We’ll define a simplified UNet model that acts as both the encoder and decoder in the diffusion process.

class UNet(nn.Module):
    def __init__(self):
        super(UNet, self).__init__()
        # Downsampling layers (Encoder)
        self.down1 = nn.Conv2d(1, 64, 3, stride=2, padding=1)   # Output: [batch_size, 64, 14, 14]
        self.down2 = nn.Conv2d(64, 128, 3, stride=2, padding=1) # Output: [batch_size, 128, 7, 7]
        
        # Bottleneck
        self.bottleneck = nn.Conv2d(128, 128, 3, padding=1)     # Output: [batch_size, 128, 7, 7]
        
        # Upsampling layers (Decoder)
        self.up1 = nn.ConvTranspose2d(128, 64, 4, stride=2, padding=1) # Output: [batch_size, 64, 14, 14]
        self.up2 = nn.ConvTranspose2d(64, 1, 4, stride=2, padding=1)   # Output: [batch_size, 1, 28, 28]
        
        # Time embedding layers
        self.time_embed = nn.Linear(1, 128)  # Embed time step t to match feature maps
        
    def forward(self, x, t):
        """
        x: Noisy input image tensor of shape [batch_size, 1, 28, 28]
        t: Time step tensor of shape [batch_size]
        """
        # Embed time step t
        t = t.float().unsqueeze(1)                  # Shape: [batch_size, 1]
        t_embed = self.time_embed(t)                # Shape: [batch_size, 128]
        t_embed = t_embed.unsqueeze(2).unsqueeze(3) # Shape: [batch_size, 128, 1, 1]
        
        # Encoder
        x1 = F.relu(self.down1(x))                  # Shape: [batch_size, 64, 14, 14]
        x2 = F.relu(self.down2(x1))                 # Shape: [batch_size, 128, 7, 7]
        
        # Add time embedding to bottleneck
        x2 = x2 + t_embed                           # Broadcasting over spatial dimensions
        
        # Bottleneck
        x3 = F.relu(self.bottleneck(x2))            # Shape: [batch_size, 128, 7, 7]
        
        # Decoder
        x4 = F.relu(self.up1(x3))                   # Shape: [batch_size, 64, 14, 14]
        x5 = torch.sigmoid(self.up2(x4))            # Shape: [batch_size, 1, 28, 28]
        
        return x5

Explanation

Downsampling (Encoder):
- down1: Reduces spatial dimensions from [28, 28] to [14, 14].
- down2: Reduces spatial dimensions from [14, 14] to [7, 7].
Time Embedding:
- self.time_embed: Embeds the time step t into a vector that can be added to the feature maps.
Bottleneck:
- Adds the time embedding to the bottleneck features.
Upsampling (Decoder):
- up1: Increases spatial dimensions from [7, 7] to [14, 14].
- up2: Increases spatial dimensions from [14, 14] to [28, 28].
Activation Functions:
- Uses ReLU activation for hidden layers.
- Uses Sigmoid activation for the output to map values between [0, 1].

Training the Diffusion Model

Hyperparameters and Setup

# Hyperparameters
num_epochs = 5
batch_size = 64
learning_rate = 1e-4
num_timesteps = 1000  # Total diffusion steps

# Beta schedule (linear)
beta = torch.linspace(0.0001, 0.02, num_timesteps).to(device) # Shape: [num_timesteps]
alpha = 1.0 - beta                                           # Shape: [num_timesteps]
alpha_hat = torch.cumprod(alpha, dim=0)                      # Shape: [num_timesteps]

beta: Defines the noise schedule.
alpha: Computed from beta.
alpha_hat: Cumulative product of alpha over time steps.

Data Loader

# Data loader
transform = transforms.Compose([transforms.ToTensor()])
dataset = datasets.MNIST(root='./data', train=True, download=True, transform=transform)
data_loader = torch.utils.data.DataLoader(dataset, batch_size=batch_size, shuffle=True)

Purpose: Load the MNIST dataset and create a data loader.

Model, Optimizer, and Loss Function

# Model, optimizer, and loss function
model = UNet().to(device)
optimizer = optim.Adam(model.parameters(), lr=learning_rate)
criterion = nn.MSELoss()

model: Instance of the UNet model.
optimizer: Adam optimizer.
criterion: Mean Squared Error loss function.

Training Loop

for epoch in range(num_epochs):
    for batch_idx, (x, _) in enumerate(data_loader):
        x = x.to(device)  # Input images: [batch_size, 1, 28, 28]

        # Sample random time steps for each image in the batch
        t = torch.randint(0, num_timesteps, (x.size(0),), device=device).long()  # Shape: [batch_size]

        # Get corresponding alpha_hat_t
        alpha_hat_t = alpha_hat[t].reshape(-1, 1, 1, 1)  # Shape: [batch_size, 1, 1, 1]

        # Sample noise
        noise = torch.randn_like(x)  # Shape: [batch_size, 1, 28, 28]

        # Generate noisy images x_t
        x_t = torch.sqrt(alpha_hat_t) * x + torch.sqrt(1 - alpha_hat_t) * noise  # Shape: [batch_size, 1, 28, 28]

        # Predict noise using the model
        noise_pred = model(x_t, t)  # Shape: [batch_size, 1, 28, 28]

        # Compute loss between the true noise and the predicted noise
        loss = criterion(noise_pred, noise)

        # Backpropagation and optimization
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()

        # Print training progress
        if batch_idx % 100 == 0:
            print(f"Epoch [{epoch+1}/{num_epochs}], Step [{batch_idx}/{len(data_loader)}], Loss: {loss.item():.4f}")

Explanation.

Sampling Time Steps:
- t: Random time steps for each image in the batch.
Computing $\alpha_hat_t$:
- Reshaped to match the dimensions of x.
Adding Noise (Forward Diffusion):
- x_t: Noisy images at time step t.
- Computed using the formula:

\[x_t = \sqrt{\hat{\alpha}_t} \cdot x_0 + \sqrt{1 - \hat{\alpha}_t} \cdot \epsilon\]

Model Prediction:
- The model predicts the noise added to the images.
Loss Calculation:
- Compares the predicted noise with the actual noise using MSE.
Optimization:
- Updates the model parameters to minimize the loss.

Inference (Sampling from the Model)

After training, we can generate new images by sampling from the model.

Sampling Function

def sample(model, num_samples, num_timesteps, device):
    model.eval()
    with torch.no_grad():
        # Start from pure noise
        x = torch.randn(num_samples, 1, 28, 28).to(device)  # Shape: [num_samples, 1, 28, 28]

        for t in reversed(range(num_timesteps)):
            t_batch = torch.tensor([t] * num_samples, device=device).long()  # Shape: [num_samples]

            alpha_t = alpha[t]
            alpha_hat_t = alpha_hat[t]
            beta_t = beta[t]

            # Predict noise
            noise_pred = model(x, t_batch)  # Shape: [num_samples, 1, 28, 28]

            # Compute coefficients
            alpha_t = alpha_t.to(device)
            alpha_hat_t = alpha_hat_t.to(device)
            beta_t = beta_t.to(device)

            # Update x
            if t > 0:
                # Predict x_{t-1} using the model's output
                x = (1 / torch.sqrt(alpha_t)) * (x - ((1 - alpha_t) / torch.sqrt(1 - alpha_hat_t)) * noise_pred)
                # Add noise
                noise = torch.randn_like(x)
                x += torch.sqrt(beta_t) * noise
            else:
                # For t = 0, no noise is added
                x = (1 / torch.sqrt(alpha_t)) * (x - ((1 - alpha_t) / torch.sqrt(1 - alpha_hat_t)) * noise_pred)
    return x

Explanation

Initialization:
- x: Starts from pure noise.
Reverse Diffusion Loop:
- Iterates from T to 0.
- t_batch: Current time step for all samples.
- Predicting Noise:
  - The model predicts the noise at each time step.
- Updating x:
  - Computes x_{t-1} using the model’s predictions.
  - Adds noise except for the final time step.
Final Output:
- Returns the denoised images.

Generating and Visualizing Samples

# Generate samples
num_samples = 16
generated_images = sample(model, num_samples, num_timesteps, device)  # Shape: [num_samples, 1, 28, 28]
generated_images = generated_images.cpu().numpy()

# Plot the generated images
fig, axes = plt.subplots(4, 4, figsize=(6, 6))
for i, ax in enumerate(axes.flatten()):
    ax.imshow(generated_images[i].squeeze(), cmap='gray')
    ax.axis('off')
plt.tight_layout()
plt.show()

Purpose: Generate a grid of generated images and display them.
Tensor Shapes:
- generated_images: [num_samples, 1, 28, 28] after conversion to NumPy.

Conclusion

We’ve provided a sample code for training and inference of a diffusion model using a simplified UNet architecture. Each line of code includes inline comments explaining its purpose and the tensor shapes involved. This example should give you a foundational understanding of how diffusion models are implemented and trained.

References

Denoising Diffusion Probabilistic Models: arXiv:2006.11239
DDPM PyTorch Implementation: GitHub Repository
Understanding Diffusion Models: Lil’Log Blog
UNet Architecture: Original Paper

Note: This code is for educational purposes and simplifies many aspects of diffusion models. For practical applications, consider using optimized libraries and more sophisticated architectures.

Sample Code for Diffusion Model Training and Inference

Table of Contents

Imports and Setup

Model Architecture (UNet)

Explanation

Training the Diffusion Model

Hyperparameters and Setup

Data Loader

Model, Optimizer, and Loss Function

Training Loop

Explanation.

Inference (Sampling from the Model)

Sampling Function

Explanation

Generating and Visualizing Samples

Conclusion

References